TWIST 6D: One Geometry, All Physics

The Heart Of the Matter

Possibility → act → window → shape.

Close your eyes and imagine: somewhere in a vast space of pure potential, something clicks. A discrete moment of becoming. That possibility, just one among infinite others, suddenly appears in a golden window. And when it does, it has a definite shape: energy, momentum, mass.

This is how reality works.

Not metaphorically. Literally. Geometrically. The world is:

- A continuous field of possibilities in ?math-inline\mathbb{C}^{3}?math-inline (quantum complex three-space) - Punctuated by discrete ontological acts (ticks) that select specific configurations - Those selections appear in the window RF³ (rhombohedral face-centered readout) - And manifest as definite energy shapes in the plane of ?math-inline(pc, mc^{2})?math-inline

Every particle. Every interaction. Every moment of your existence.

Possibility → act → window → shape.

---

The Journey: Four Stations of Reality

Imagine reality as a journey with four stations:

?math-inline \mathbb{C}^{3} \quad\to\quad \text{tick} \quad\to\quad \text{RF}^{3} \quad\to\quad \text{Energy} ?math-inline

?math-inline \text{(possibility)} \quad\to\quad \text{(selection)} \quad\to\quad \text{(actuality)} \quad\to\quad \text{(shape)} ?math-inline

Station 1: The Field of All Possibilities

**?math-inline\mathbb{C}^{3}?math-inline ** = complex three-space

Picture this: Not ordinary 3D space, but complex 3D. Each coordinate isn't just a number. It's a number with both real and imaginary parts. A number that encodes both "where" and "configuration."

This is the quantum field. Not a field in space, but the field that becomes space when observed. Here, everything that could happen coexists. All possible configurations. All potential states. Schrödinger's wavefunction ?math-inline\Phi(z)?math-inline rippling across six real dimensions organized as three complex pairs.

Imagination prompt: Think of ?math-inline\mathbb{C}^{3}?math-inline as an infinite ocean where every wave is a possibility, every ripple a potential future, every interference pattern a quantum superposition. Nothing is "decided" yet. Everything could be.

Station 2: The Ontological Act

The Tick = discrete moment of becoming

Time doesn't flow here. Reality clicks.

Each click is a discrete step: ?math-inlinet = n\tau?math-inline where ?math-inlinen?math-inline counts transitions. Between clicks: the possibility field evolves according to geometric rules. At each click: a selection happens. One configuration out of infinite possibilities becomes actual.

This isn't measurement by an external observer. This is reality making itself definite through its own geometric dynamics.

Imagination prompt: Like a cosmic heartbeat. Each beat: the entire universe updates. Between beats: quantum possibilities ripple and evolve. At each beat: one configuration crystallizes into existence. Click. Click. Click. The rhythm of becoming.

This is where quantum mechanics comes from. The "collapse" isn't mysterious. It's geometric necessity. Reality can't remain pure superposition forever. It must click into definiteness.

Station 3: The Golden Window

RF³ = rhombohedral face-centered projection

After the tick selects a configuration, that configuration must pass through a window to become observable.

The window ?math-inlineW?math-inline is a rhombic triacontahedron, thirty golden rhombic faces, each built from ?math-inline\varphi?math-inline -ratios. Only when the imaginary coordinates ?math-inlineu?math-inline fall inside this golden structure does the real coordinate ?math-inlinex?math-inline become actual.

?math-inline \rho(x) = \int_{u\in W} |\Phi(x+iu)|^{2}\, d^{3}u ?math-inline

The integration over ?math-inlineW?math-inline is like shining light through a crystal, only certain angles pass through, creating the pattern we call "observable reality."

Imagination prompt: Picture a thirty-faceted golden crystal floating in imaginary space. Reality (?math-inline\mathbb{C}^{3}?math-inline ) shines through it. What emerges on the other side is our 3D world. The crystal doesn't just filter. It constitutes what can exist. Without the window, there is no actuality, only unmanifested potential.

This is where Einstein's relativity comes from. Space isn't a pre-existing container. It's the projection pattern that emerges from ?math-inline\mathbb{C}^{3}?math-inline through golden window ?math-inlineW?math-inline . The geometry of ?math-inlineW?math-inline determines spacetime structure.

Station 4: The Energy Shape

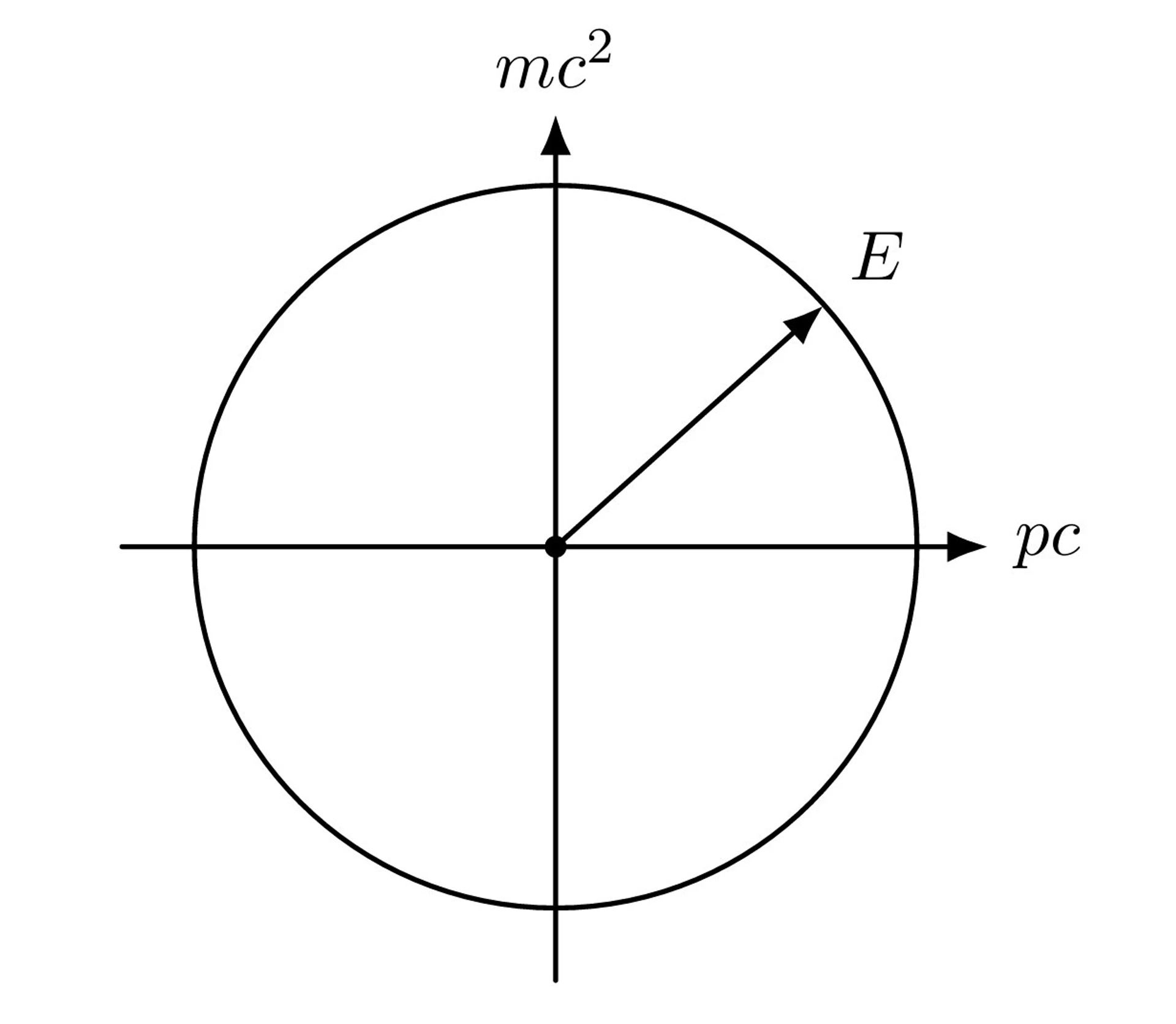
The Pythagorean Circle = ?math-inlineE^{2} = (pc)^{2} + (mc^{2})^{2}?math-inline

Every actualized configuration has an energy. And that energy has a beautiful geometric form: a circle in the plane of (momentum, mass).

mc² ↑ | -----(•)----→ pc |

E² = (pc)² + (mc²)²

This is Pythagoras's theorem! But not in ordinary space, in energy-momentum space. The hypotenuse ?math-inlineE?math-inline is total energy. The legs are momentum-energy ?math-inline(pc)?math-inline and rest-energy ?math-inline(mc^{2})?math-inline .

Every particle lives somewhere on this circle.

- Pure energy (photons): maximum ?math-inlinepc?math-inline , zero mass → circle's equator - Pure mass (slow particles): zero ?math-inlinepc?math-inline , maximum ?math-inlinemc^{2}?math-inline → circle's pole - Everything else: somewhere in between

Imagination prompt: Each particle is a point on a vast circle. Massless particles race around the rim at speed ?math-inlinec?math-inline . Massive particles cluster near the poles. The circle itself? It's the natural shape of being, the geometry that emerges when possibility becomes actuality through the golden window.

This unifies relativity and quantum mechanics. ?math-inlineE = mc^{2}?math-inline (Einstein) and ?math-inlineE = \hbar\omega?math-inline (Planck) both emerge from the same circular geometry in ?math-inline(pc, mc^{2})?math-inline space.

---

The Rosetta: How 6D Projects to 3D

Sir Penrose showed how to project 5D cube to never repeating tiles. TWIST does the same, just one dimension extra: from 6D to 3D with the same mathematics principles underlying the magic.

Reality isn't really "six-dimensional." It's three complex dimensions: ?math-inlinez = x + iu?math-inline where ?math-inlinez \in \mathbb{C}^{3}?math-inline .

But to calculate with it, we work with six real coordinates: ?math-inline(x_{1}, x_{2}, x_{3}, u_{1}, u_{2}, u_{3})?math-inline .

The golden transformation (the Rosetta) mixes real and imaginary pairs using ?math-inline\varphi?math-inline :

For each coordinate pair ?math-inline(x_k, u_k)?math-inline , define:

?math-inline \begin{pmatrix}U_{k}\\ V_{k}\end{pmatrix} = \frac{1}{\sqrt{1+\varphi^{2}}} \begin{pmatrix} 1 & \varphi\\ -\varphi & 1 \end{pmatrix} \begin{pmatrix}x_{k}\\ u_{k}\end{pmatrix}, \quad k=1,2,3 ?math-inline

Where ?math-inline\varphi = (1+\sqrt{5})/2?math-inline is the golden ratio.

This gives us:

- U-coordinates ?math-inline(U_{1}, U_{2}, U_{3})?math-inline : What we observe in RF³ - the "readout" axis - V-coordinates ?math-inline(V_{1}, V_{2}, V_{3})?math-inline : The gating condition: the "orthogonal" filter

The rotation is ?math-inlineO(6)?math-inline , so ?math-inline\mathbf{U} \cdot \mathbf{V} = 0?math-inline and lengths are preserved.

Acceptance window: Visibility is ?math-inline\mathbf{V} \in W?math-inline , where ?math-inlineW?math-inline is the rhombic triacontahedron window used throughout the canon. (For intuition, a radial ball ?math-inline\|\mathbf{V}\| \leq W_{0}?math-inline can serve as a toy filter, but all quantitative results:?math-inline\alpha?math-inline , ?math-inlineG?math-inline use the polyhedral ?math-inlineW?math-inline .)

Imagination prompt: Every point in 6D reality gets sorted by this golden sieve. The ?math-inlineU?math-inline -coordinates tell you where it appears. The ?math-inlineV?math-inline -coordinates tell you if it appears. Golden ratio mixing ensures maximum richness without periodic resonance, the most complex stable structure possible.

This is akin to Penrose aperiodicity in 3D. Roger Penrose discovered you could tile a plane non-periodically using golden ratios. We're doing something similar in three dimensions, with complex coordinates, using it to generate observable reality itself.

---

Energy Conservation: The Miracle of Projection

Here's something remarkable: Energy is preserved through projection.

In full 6D (?math-inline\mathbb{C}^{3}?math-inline ), energy is:

?math-inline E_{6D} = \frac{\hbar c}{a}\,\sqrt{L^{2} + M^{2}} ?math-inline

Where:

- ?math-inlineL = a|\nabla_{x}\theta|?math-inline (light-axis component, from real gradients) - ?math-inlineM = a|\nabla_{u}\theta|?math-inline (matter-axis component, from imaginary gradients)

When we project through the Rosetta to RF³:

?math-inline E_{\text{RF}^{3}} = \sqrt{(pc)^{2} + (mc^{2})^{2}} ?math-inline

Where:

- ?math-inlinep = (\hbar/a)L?math-inline (momentum) - ?math-inlinemc = (\hbar/a)M?math-inline (rest mass-energy)

**These are identical: ?math-inlineE_{6D} = E_{\text{RF}^{3}}?math-inline **

The dictionary:?math-inline L = \frac{ap}{\hbar}, \quad M = \frac{amc}{\hbar}, \quad E = \frac{\hbar c}{a}\sqrt{L^{2}+M^{2}} \Rightarrow E^{2} = (pc)^{2}+(mc^{2})^{2} ?math-inline $

Why? Because the Rosetta rotation is orthogonal (an ?math-inlineO(6)?math-inline matrix). It preserves lengths and angles. The golden window ?math-inlineW?math-inline filters (selects which ?math-inline\mathbf{V}?math-inline -coordinates pass) but doesn't rescale (preserves the gradients).

What this means:

When possibility becomes actuality, nothing is lost or gained. The energy you measure in 3D is the same energy that existed in 6D potential. The projection is lossless. Reality doesn't "collapse" into a lower-energy state, it remains perfectly consistent through the transformation.

The Mathematical Proof:

The Rosetta satisfies:?math-inline PP^{\top}=I_{3},\qquad P^{\perp}(P^{\perp})^{\top}=I_{3},\qquad PP^{\perp\top}=0 ?math-inline

Therefore gradients transform isometrically:

?math-inline |\nabla_{x}\theta| = |\nabla_{U}\theta|, \qquad |\nabla_{u}\theta| = |\nabla_{V}\theta| ?math-inline

Since the window only selects (doesn't rescale):?math-inline L_{\text{RF}} = L, \qquad M_{\text{RF}} = M ?math-inline

Substitution yields:

?math-inline E_{6D} = \frac{\hbar c}{a}\sqrt{L^{2}+M^{2}} = \sqrt{(pc)^{2} + (mc^{2})^{2}} = E_{\text{RF}^{3}} ?math-inline

Proposition (Energy Preservation): Projection through the golden Rosetta and the window ?math-inlineW?math-inline preserves energy exactly.

Imagination prompt: Like a hologram, the 2D surface encodes all the 3D information. When you view it at the right angle (through golden window ?math-inlineW?math-inline ), the full 3D image appears, with all its depth and structure intact. No information lost. No energy added or removed. Just... transformation of perspective.

The √-Light Rotor (How the Circle Updates)

Want to see the energy circle in motion? Define the first-order operator:

?math-inline H_{0} = \frac{\hbar c}{a}(L\sigma_{x} + M\sigma_{z}) ?math-inline

Then ?math-inlineH_{0}^{2} = (\hbar c/a)^{2}(L^{2}+M^{2})\mathbf{1}?math-inline and the tick update is:

?math-inline \Psi_{n+1} = e^{-i\tau H_{0}/\hbar}\Psi_{n} ?math-inline

This two-component rotor recovers the circle eigen-energies directly. The discrete clicks rotate the state around the Pythagorean circle in ?math-inline(L,M)?math-inline space, exactly what you'd expect from the geometric picture.

---

---

The Fine Structure Constant: Pure Geometry

From the three primitive scales ?math-inlineI?math-inline (inertia), ?math-inlineK?math-inline (stiffness), ?math-inlinea?math-inline (length), everything flows:?math-inline c = a\sqrt{\frac{K}{I}} \quad\text{(speed of light: geometric ratio)} ?math-inline $

?math-inline \eta = \sqrt{IK} \quad\text{(action invariant)} ?math-inline

?math-inline \hbar = q\eta \quad\text{(Planck's constant: quantum angle times action)} ?math-inline

But the fine structure constant ?math-inline\alpha?math-inline ? In this framework, it's purely geometric, all the mechanical scales cancel:

?math-inline \alpha^{-1} = 24\pi^{2} \sin\left(\frac{\pi}{5}\right) \cdot r_{*}(W) ?math-inline

Where ?math-inliner_{*}(W)?math-inline is the Rosetta projection integral, an average over the twelve golden icosahedral directions. Detailed derivation, error analysis, and assumptions are provided in the companion papers (see References).

No ?math-inlineI?math-inline . No ?math-inlineK?math-inline . No ?math-inlinea?math-inline . No ?math-inline\hbar?math-inline . No ?math-inlinec?math-inline .

Just geometry: Golden angles. Icosahedral symmetry. The window ?math-inlineW?math-inline .

**We propose that ?math-inline\alpha = 1/137.036?math-inline emerges because that's the impedance of a rhombic triacontahedron window with ?math-inline\varphi?math-inline -ratios averaged over icosahedral symmetry.**

Imagination prompt: The universe has an "electrical resistance": how hard is it for light to interact with matter? Turns out, that resistance is a shape. The shape of the golden window through which actuality flows. Change the shape, change the constant. But there's only one self-consistent shape for stable reality: the thirty-faced golden crystal.

---

Newton's Constant: The Weight of Actuality

Gravity in TWIST isn't curvature of spacetime (though it looks like that in RF³). It's the **elastic response of the ?math-inline\mathbb{C}^{3}?math-inline field** to localized energy concentrations.

Using discrete exterior calculus (DEC) on the golden lattice structure:

?math-inline G = \frac{a^{2}c^{3}}{\hbar}\,\frac{1}{g_{\text{geo}}(W)} = \frac{q}{128\pi\sin\left(\frac{\pi}{5}\right)}\,\frac{c^{3}a^{2}}{\hbar} ?math-inline

The factor ?math-inline128\pi?math-inline comes from:

- 4: weak-field calibration (?math-inlineU = c^{2}\phi/4?math-inline ) - 8: node volume (?math-inlinea^{3}/8?math-inline per lattice site) - 4: longitudinal projection (gravity is scalar, not vector) - **?math-inline\pi?math-inline **: Coulomb kernel (?math-inline1/r?math-inline potential)

Everything else? Golden geometry again: ?math-inline\sin(\pi/5)?math-inline from icosahedral angles, ?math-inlineq?math-inline from quantum discrete step.

The Planck length emerges:

?math-inline \frac{a}{\ell_{P}} = 8\varphi\sqrt{\sin\left(\frac{\pi}{5}\right)} ?math-inline

The lattice scale ?math-inlinea?math-inline and Planck length ?math-inline\ell_{P}?math-inline are related by golden ratio geometry!

Imagination prompt: Mass tells the ?math-inline\mathbb{C}^{3}?math-inline field how to bend. The field tells mass how to move. But "bending" isn't curvature of space. It's modulation of the ?math-inlineI?math-inline and ?math-inlineK?math-inline parameters while preserving the invariants ?math-inline\eta?math-inline and ?math-inlinec?math-inline . The apparent curvature is what this looks like when observed through RF³. Einstein's equations are the shadow of deeper discrete mechanics.

Gravity is weak because: The golden window geometry makes it so. The same ?math-inlineW?math-inline that gives ?math-inline\alpha = 1/137?math-inline also makes ?math-inlineG?math-inline tiny. Not coincidence, but geometric necessity.

---

The Bridge: Connecting EM and Gravity

Let ?math-inlineb = amc/\hbar?math-inline be the spectral gap (dimensionless mass).

Gravitational coupling:?math-inline \alpha_{G} = \frac{Gm^{2}}{\hbar c} = \kappa_{G} \cdot b^{2} ?math-inline

Electromagnetic coupling: ?math-inline\alpha?math-inline (from above)

The bridge:

?math-inline \boxed{\alpha_{G} = \alpha \cdot B \cdot b^{2}} ?math-inline

Where

?math-inline B = \frac{3\pi q}{16}\,r_{*}(W) = \frac{\kappa_{G}}{\alpha} ?math-inline

Same window. Same geometry. Two forces connected.

Why is gravity so much weaker than electromagnetism?

Because: The bridge factor ?math-inlineB?math-inline multiplies ?math-inline\alpha?math-inline by the spectral gap squared. For typical particles, ?math-inlineb^{2}?math-inline is enormous, but ?math-inlineB?math-inline is tiny. The golden window geometry suppresses gravitational coupling relative to electromagnetic.

Imagination prompt: Imagine two cosmic dials. One controls light-matter coupling (?math-inline\alpha?math-inline ). One controls gravity coupling (?math-inline\alpha_{G}?math-inline ). They're not independent. They're geared together through golden ratio geometry. Turn one, and the other must turn in a specific way determined by the window ?math-inlineW?math-inline . The universe isn't fine-tuned. It's geometrically constrained.

---

Einstein and Quantum: Both Projections

Einstein's Relativity

**Why is ?math-inlinec?math-inline constant? Why does ?math-inlineE = mc^{2}?math-inline ? Why does gravity curve spacetime?**

TWIST answer: These aren't separate postulates. They're all consequences of RF³ projection from ?math-inline\mathbb{C}^{3}?math-inline .

- **?math-inlinec?math-inline is constant** because it's the geometric ratio ?math-inlinec = a\sqrt{K/I}?math-inline , and ?math-inlineK/I?math-inline is preserved by the click dynamics - **?math-inlineE = mc^{2}?math-inline ** because energy and mass live on the Pythagorean circle in ?math-inline(pc, mc^{2})?math-inline space - Spacetime curves because varying ?math-inlineI?math-inline and ?math-inlineK?math-inline (while preserving ?math-inline\eta?math-inline and ?math-inlinec?math-inline ) looks like metric variation in RF³

Einstein discovered the geometry of actuality (how RF³ behaves). He didn't know about the ?math-inline\mathbb{C}^{3}?math-inline substrate. But his equations are exactly right for the projected reality.

Quantum Mechanics

Why wavefunctions? Why probability? Why measurement "collapse"? Why is observation special?

TWIST answer:

- Wavefunctions because reality is literally a field ?math-inline\Phi(z)?math-inline on ?math-inline\mathbb{C}^{3}?math-inline - "Probability" because we only see projections through ?math-inlineW?math-inline statistics of ?math-inlineu \in W?math-inline - "Collapse" because ticks are discrete selection events, not continuous evolution - Observation is special because it's literally the RF³ projection, the geometric act that constitutes actuality

Heisenberg discovered the mechanics of possibility (how ?math-inline\mathbb{C}^{3}?math-inline field evolves between ticks). He didn't know about RF³ window. But his uncertainty relations are exactly right for complex 3-space dynamics.

Both were right. Both were incomplete. TWIST unifies them.

---

General Relativity: Spacetime as Projection Shadow

Einstein told us gravity isn't a force, but it's the curvature of spacetime. Massive objects bend spacetime, and other objects follow the curves.

But what IS spacetime in TWIST?

Spacetime Doesn't Exist Fundamentally

In this framework, there is no pre-existing spacetime "fabric" that gets curved. Instead:

Spacetime is the readout pattern that emerges when you observe ?math-inline\mathbb{C}^{3}?math-inline through the golden window ?math-inlineW?math-inline .

Think about it:

- Space = the real coordinates ?math-inlinex?math-inline you observe when ?math-inlineu \in W?math-inline - Time = the causal sequence of discrete clicks ?math-inlinet = n\tau?math-inline - Spacetime = the 3+1 dimensional pattern these create

How Curvature Emerges

In ?math-inline\mathbb{C}^{3}?math-inline , the fundamental parameters are ?math-inlineI?math-inline (inertia), ?math-inlineK?math-inline (stiffness), and ?math-inlinea?math-inline (lattice scale). These determine:

?math-inline c = a\sqrt{\frac{K}{I}}, \qquad \eta = \sqrt{IK}, \qquad \hbar = q\eta ?math-inline

**But ?math-inlineI?math-inline and ?math-inlineK?math-inline can vary in space!** When they do, while preserving the invariants ?math-inline\eta?math-inline and ?math-inlinec?math-inline , something remarkable happens:

In RF³, this looks exactly like spacetime curvature.

The Mechanism

Consider a region with varying inertia ?math-inlineI(x)?math-inline and stiffness ?math-inlineK(x)?math-inline :

1. Preserve action invariant: ?math-inline\eta(x) = \sqrt{I(x)K(x)} = \text{constant}?math-inline 2. Preserve speed: ?math-inlinec(x) = a\sqrt{K(x)/I(x)} = \text{constant}?math-inline

This means: ?math-inlineI?math-inline and ?math-inlineK?math-inline must vary together in a specific correlated way.

From the RF³ perspective:

- Varying ?math-inlineI?math-inline looks like varying "density" of the field - Varying ?math-inlineK?math-inline looks like varying "tension" of the field - Together, they create an effective metric ?math-inlineg_{\mu\nu}(x)?math-inline

The field equations in ?math-inline\mathbb{C}^{3}?math-inline that govern how ?math-inlineI?math-inline and ?math-inlineK?math-inline respond to energy concentrations project to Einstein's field equations in RF³:

?math-inline G_{\mu\nu} = 8\pi G \, T_{\mu\nu} ?math-inline

Where:

- ?math-inlineG_{\mu\nu}?math-inline (Einstein tensor) = geometric projection of lattice elastic response - ?math-inlineT_{\mu\nu}?math-inline (stress-energy) = local concentration of energy-momentum - ?math-inlineG?math-inline (Newton's constant) = elastic modulus of the window geometry

What This Means

Einstein discovered the shadow.

General relativity correctly describes how RF³ (observable reality) behaves. But it's describing the projection, not the underlying reality.

- Black holes: Extreme variations in ?math-inlineI?math-inline and ?math-inlineK?math-inline that create apparent singularities in RF³ projection - Gravitational waves: Ripples in the ?math-inlineI,K?math-inline field propagating through ?math-inline\mathbb{C}^{3}?math-inline , projected as spacetime oscillations - Cosmological expansion: Global evolution of average ?math-inlineI,K?math-inline values, appearing as metric expansion - Dark energy: Perhaps baseline tension in the ?math-inlineK?math-inline field (cosmological constant)

Imagination prompt: Picture a rubber sheet (the usual GR analogy). But now realize: the sheet itself isn't fundamental. It's what you see when you project a 6-parameter elastic field through a golden window. The "bending" you see is real in RF³, but it's encoding deeper geometric relationships in ?math-inline\mathbb{C}^{3}?math-inline .

Why Einstein's Equations Work

The genius of Einstein was discovering the correct geometric description of the projection. His equations are exactly right for RF³ physics. He didn't need to know about:

- Complex 3-space substrate - Discrete clicks - Golden window projection - Underlying ?math-inlineI,K?math-inline mechanics

The projection is self-consistent. You can do all of physics in RF³ using GR, and it works perfectly, because that's what we observe.

But now we know: Curvature is not fundamental. It's the geometric appearance of elastic response in a deeper discrete structure.

---

Bell's Theorem: Interference from Complex Space

The most famous "spooky action at a distance." Two particles, separated by vast distances, measured at different angles. Their results are correlated in ways that seem impossible.

Bell's inequality says: If particles have definite properties before measurement (realism) and can't communicate faster than light (locality), then correlations must satisfy:

?math-inline |S| \leq 2 ?math-inline

Quantum mechanics predicts:

?math-inline |S| = 2\sqrt{2} \approx 2.828 ?math-inline

Experiments measure: ?math-inline|S| \approx 2.7?math-inline to ?math-inline2.8?math-inline : quantum mechanics wins!

The Standard Mystery

This seems to force a choice:

1. Give up realism: Particles don't have properties until measured 2. Give up locality: Measuring one particle instantly affects the other 3. Give up free will: Measurement choices aren't independent

The TWIST Resolution: It's Interference

In this framework, none of the above. The Bell violation isn't mysterious communication. It's geometric interference from the projection from ?math-inline\mathbb{C}^{3}?math-inline to RF³.

How It Works

Consider two particles A and B in an entangled state. In ?math-inline\mathbb{C}^{3}?math-inline :

?math-inline |\Psi\rangle = \frac{1}{\sqrt{2}}\big(|0\rangle_A |1\rangle_B - |1\rangle_A |0\rangle_B\big) ?math-inline

This is a **single wavefunction on ?math-inline\mathbb{C}^{3}?math-inline **, not two separate particles. It encodes correlations in the complex coordinates.

**When you measure at angles ?math-inline\alpha?math-inline and ?math-inline\beta?math-inline :**

The correlation you observe is:

?math-inline E(\alpha,\beta) = -\cos\big(2(\alpha-\beta)\big) ?math-inline

This gives the CHSH parameter:

?math-inline S = E(\alpha,\beta) + E(\alpha,\beta') + E(\alpha',\beta) - E(\alpha',\beta') ?math-inline

With optimal angles ?math-inline(0°, 45°, 22.5°, -22.5°)?math-inline : **?math-inlineS = 2\sqrt{2}?math-inline **

Why does this violate Bell's bound?

The Double-Slit Connection

Bell violations are exactly analogous to double-slit interference:

Double-slit:

- Single particle passes through two slits - Wavefunction: ?math-inline\Psi = \Psi_1 + \Psi_2?math-inline (complex amplitudes) - Intensity: ?math-inline|\Psi|^2 = |\Psi_1|^2 + |\Psi_2|^2 + 2\text{Re}(\Psi_1^* \Psi_2)?math-inline - The interference term ?math-inline2\text{Re}(\Psi_1^* \Psi_2)?math-inline creates the pattern - You can't explain it by saying "particle went through slit 1 OR slit 2"

Bell test:

- Single joint wavefunction for both particles - State: ?math-inline\Psi = \Psi_{01} - \Psi_{10}?math-inline (complex amplitudes) - Correlation: ?math-inlineE(\alpha,\beta) = -\cos(2(\alpha-\beta))?math-inline (interference pattern) - The correlation emerges from amplitude interference in ?math-inline\mathbb{C}^{3}?math-inline - You can't explain it by saying "particle A has value ?math-inline\pm 1?math-inline AND particle B has value ?math-inline\pm 1?math-inline "

Why Classical Models Fail

Classical thinking: Each particle has a definite value ?math-inlineA = \pm 1?math-inline and ?math-inlineB = \pm 1?math-inline (hidden variables). Then correlations are just averages of products.

Problem: You're adding probabilities instead of amplitudes.

When you add probabilities, you get ?math-inline|S| \leq 2?math-inline (Bell bound).

When you add complex amplitudes (and let them interfere), you get ?math-inline|S| = 2\sqrt{2}?math-inline (Tsirelson bound).

The Projection Mechanism

Here's what's actually happening in TWIST:

1. **In ?math-inline\mathbb{C}^{3}?math-inline **: The joint state ?math-inline\Psi(z_A, z_B)?math-inline exists as a single field 2. Measurement operators ?math-inlineM_\alpha?math-inline and ?math-inlineM_\beta?math-inline project through the window ?math-inlineW?math-inline 3. Interference occurs in the complex coordinates during projection 4. Observable correlations in RF³ reflect this interference pattern

The "spooky action" is no more mysterious than double-slit interference. It's the same phenomenon:

**Complex amplitudes on ?math-inline\mathbb{C}^{3}?math-inline interfere when projected to observable RF³.**

No Faster-Than-Light Communication

Crucially, you cannot use Bell correlations to send information:

- Alice's measurement gives random result (50/50) - Bob's measurement gives random result (50/50) - Only when they compare results do they see the correlation

This is guaranteed by the no-signaling theorem: Local operations on ?math-inlineA?math-inline don't change the marginal distribution on ?math-inlineB?math-inline .

In TWIST language: Projection through ?math-inlineW?math-inline at location ?math-inlineA?math-inline is independent of projection at location ?math-inlineB?math-inline . The correlations exist in the joint wavefunction on ?math-inline\mathbb{C}^{3}?math-inline , but observing one location doesn't transmit information to the other.

Why 2√2 Specifically?

The Tsirelson bound ?math-inline2\sqrt{2}?math-inline isn't arbitrary. It comes from:

1. Unitarity of quantum mechanics (probability conservation) 2. Information causality (can't extract more information than was sent) 3. Complex geometry of ?math-inline\mathbb{C}^{3}?math-inline projection

If nature violated it more (say, ?math-inlineS = 4?math-inline ), you could use quantum correlations to transmit information superluminally. The universe "stops" at ?math-inline2\sqrt{2}?math-inline to preserve causality.

In TWIST: The golden window geometry and discrete click structure automatically enforce the Tsirelson bound. It's not added as a postulate. It emerges from the projection mathematics.

All Quantum "Weirdness" is Interference

Every supposedly mysterious quantum phenomenon is the same thing:

- Superposition: Wavefunction on ?math-inline\mathbb{C}^{3}?math-inline before projection - Collapse: Discrete click selects configuration, projects through ?math-inlineW?math-inline - Uncertainty: You can't know both position and momentum because they're conjugate projections - Entanglement: Joint wavefunctions with interference terms - Tunneling: Complex coordinates allow "paths" forbidden in real space - Vacuum fluctuations: ?math-inline\mathbb{C}^{3}?math-inline field never completely vanishes

They're all the same phenomenon: Complex 3-space projecting to observable 3D.

The Beauty of TWIST's Resolution

Traditional interpretations fight over what Bell violations "mean":

- Copenhagen: Collapse is fundamental - Many-worlds: All outcomes occur - Bohmian: Hidden variables + nonlocality - Superdeterminism: No free will

TWIST says: Stop fighting. It's just interference. Complex amplitudes on ?math-inline\mathbb{C}^{3}?math-inline project to RF³. That projection has interference terms. Those terms create correlations. No mystery.

Imagination prompt: Imagine watching shadows on a wall (Plato's cave again). Two shadows move in correlated ways, spinning together, stopping together. You might think they're communicating somehow. But actually, they're both shadows of a single object rotating in 3D. The correlation exists in the higher-dimensional object, not in communication between shadows.

Bell correlations are shadows of a single wavefunction on ?math-inline\mathbb{C}^{3}?math-inline . The "spooky correlation" exists in the complex space, not in RF³ communication.

---

The Grand Unification: QM + GR + Bell

Let's connect all three:

Quantum Mechanics

- What it discovered: Wave dynamics on ?math-inline\mathbb{C}^{3}?math-inline - What it describes: Evolution between discrete clicks - Key insight: Reality is fundamentally wavelike (complex amplitudes) - Incomplete because: Didn't know about RF³ projection and discrete time

General Relativity

- What it discovered: Geometric description of RF³ - What it describes: How observable spacetime responds to energy - Key insight: Gravity is geometry (of the projection) - Incomplete because: Didn't know about ?math-inline\mathbb{C}^{3}?math-inline substrate and ?math-inlineI,K?math-inline mechanics

Bell's Theorem Violation

- What it discovered: Correlations exceed classical bounds - What it describes: Interference patterns in complex→real projection - Key insight: Reality can't be separated into independent parts - Incomplete because: Mistook interference for mysterious nonlocality

TWIST 6D Unifies All Three

One framework. One projection. One physics.

The apparently separate phenomena—quantum waves, spacetime curvature, nonlocal correlations—are all the same thing viewed from different angles:

**?math-inline\mathbb{C}^{3}?math-inline (possibility) → discrete clicks (selection) → golden window ?math-inlineW?math-inline (projection) → RF³ (actuality)**

Einstein and Bohr were both right. They were looking at different aspects of the same projection:

- Einstein saw the geometric projection (GR) - Bohr saw the wave interference (QM) - Bell proved they can't both be classical - TWIST shows they're both projections from complex 3-space

---

The Shape of Things

Possibility → act → window → shape.

Every particle that exists made this journey.

Every photon, every electron, every atom in your body: started as pure potential in ?math-inline\mathbb{C}^{3}?math-inline , got selected by a quantum tick, projected through golden window ?math-inlineW?math-inline , and manifested as a definite energy shape on the Pythagorean circle.

You are reading these words because:

- Complex 3-space allows rich wave structures (?math-inline\mathbb{C}^{3}?math-inline ) - Discrete ticks actualize configurations (?math-inlinet = n\tau?math-inline ) - Golden window permits stable observation (?math-inlineW?math-inline ) - Energy circle determines possible states (?math-inlineE^{2} = (pc)^{2} + (mc^{2})^{2}?math-inline )

Reality doesn't just exist. It becomes, moment by moment, tick by tick, through the golden gateway between potential and actual.

And the constants that govern all of this? They're not arbitrary. They're the impedance and elastic modulus of the golden window itself.

**?math-inline\alpha = 137.036?math-inline isn't mysterious. It's inevitable.**

**?math-inlineG?math-inline isn't fine-tuned. It's geometric.**

Spacetime isn't fundamental. It's projection.

**Quantum mechanics isn't weird. It's ?math-inline\mathbb{C}^{3}?math-inline .**

Welcome to TWIST 6D QIK.

The universe is mechanical. And it's beautiful. Always the same. Forever new.

---

Technical Summary

For those who want the explicit mathematics:

Rosetta projection: Golden ratio mixing of real/imaginary coordinate pairs preserves energy through orthogonal ?math-inlineO(6)?math-inline rotation

?math-inline \begin{pmatrix}U_{k}\\ V_{k}\end{pmatrix} = \frac{1}{\sqrt{1+\varphi^{2}}} \begin{pmatrix} 1 & \varphi\\ -\varphi & 1 \end{pmatrix} \begin{pmatrix}x_{k}\\ u_{k}\end{pmatrix}, \qquad k=1,2,3 ?math-inline

Window function: ?math-inlineW?math-inline is the rhombic triacontahedron that filters ?math-inline\mathbf{V}?math-inline -coordinates. (Ball ?math-inline\|\mathbf{V}\| \leq W_{0}?math-inline is pedagogical toy only.)

Energy preservation:

?math-inline E_{6D} = \frac{\hbar c}{a}\sqrt{L^{2}+M^{2}} = \sqrt{(pc)^{2} + (mc^{2})^{2}} = E_{\text{RF}^{3}} ?math-inline

Where ?math-inlineL = ap/\hbar?math-inline (light-axis), ?math-inlineM = amc/\hbar?math-inline (matter-axis).

Fine structure:

?math-inline \alpha^{-1} = 24\pi^{2} \sin\left(\frac{\pi}{5}\right) \cdot r_{*}(W) \approx 137.036 ?math-inline

Newton constant:

?math-inline G = \frac{q}{128\pi\sin\left(\frac{\pi}{5}\right)} \cdot \frac{c^{3}a^{2}}{\hbar} ?math-inline

Bridge relation:

?math-inline \alpha_{G} = \alpha \cdot B \cdot b^{2} \quad\text{where}\quad B = \frac{3\pi q}{16}\,r_{*}(W) ?math-inline

General Relativity emergence:

Varying inertia ?math-inlineI(x)?math-inline and stiffness ?math-inlineK(x)?math-inline while preserving invariants:

?math-inline \eta(x) = \sqrt{I(x)K(x)} = \text{const}, \qquad c(x) = a\sqrt{K(x)/I(x)} = \text{const} ?math-inline

Projects to effective metric ?math-inlineg_{\mu\nu}(x)?math-inline satisfying Einstein's equations:

?math-inline G_{\mu\nu} = 8\pi G \, T_{\mu\nu} ?math-inline

Bell correlations:

For polarization measurements at angles ?math-inline\alpha, \beta?math-inline (note: polarization uses ?math-inline-\cos(2\Delta)?math-inline ; spin-½ uses ?math-inline-\cos(\Delta)?math-inline ):

?math-inline E(\alpha,\beta) = -\cos\big(2(\alpha-\beta)\big) ?math-inline

CHSH parameter with optimal angles:

?math-inline S = E(\alpha,\beta) + E(\alpha,\beta') + E(\alpha',\beta) - E(\alpha',\beta') = 2\sqrt{2} ?math-inline

Measurement operators on transverse light sector:

?math-inline M_{\theta} = |\theta\rangle\langle\theta| - |\theta+\tfrac{\pi}{2}\rangle\langle\theta+\tfrac{\pi}{2}| ?math-inline $

Tsirelson bound emerges from projection geometry and information causality.

√-Light rotor:

?math-inline H_{0} = \frac{\hbar c}{a}(L\sigma_{x} + M\sigma_{z}), \quad H_{0}^{2} = \left(\frac{\hbar c}{a}\right)^{2}(L^{2}+M^{2})\mathbf{1} ?math-inline $

Tick update: ?math-inline\Psi_{n+1} = e^{-i\tau H_{0}/\hbar}\Psi_{n}?math-inline reproduces energy circle.